You are given an array of integers representing the lengths of several ropes. Your task is to connect all the ropes into a single rope with the minimum possible cost. The cost of connecting two ropes is the sum of their lengths. Write an algorithm to Connect Multiple Ropes With Minimum Cost.

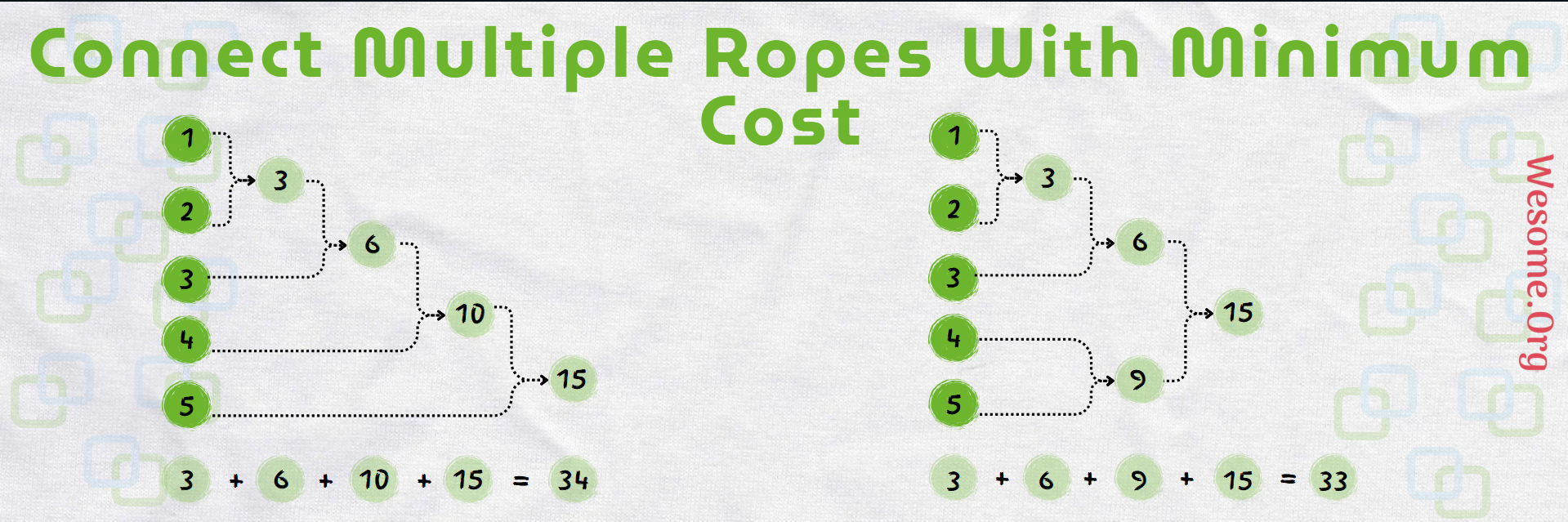
The strategy is to always connect the two smallest ropes first, as they contribute more to the total cost when picked earlier. This approach, similar to Huffman Coding, minimizes the cost by combining smaller elements first.

The Min-Heap implementation is similar to Huffman Coding,  ie minimizes the cost by combining smaller elements first.

To implement the approach, use a Min-Heap, also known as a Priority Queue, to store the rope lengths. Keep iterating the queue until only 1 element is left, extract the two smallest values, sum them, and insert the sum back into the min-heap. Track the total cost by adding the sum at each step, and return the total cost when only one element remains in the min-heap.
 

Code Flow for Connect Multiple Ropes With Minimum Cost

1. Initialize a priority queue pq to store the rope lengths.
2. Add all elements from the input array arr to the priority queue.
3. There is more than one element in the priority queue:
   • Remove the two smallest rope lengths (ropeOne and roteTwo) from the priority queue.
   • Calculate the combined length (combine) by adding ropeOne and roteTwo.
   • Update the result variable by adding the combined length (combine) to it.
   • Add the combined length back into the priority queue.
4. Return the calculated minimum cost (result).

5. End.

1. Let's see the code now

package org.wesome.dsalgo;

import java.util.Objects;
import java.util.PriorityQueue;


public class MinCostRope {
    static int minCostRope(int[] arr) {
        if (Objects.isNull(arr)) {
            throw new NullPointerException("array is null");
        }
        int size = arr.length;
        /*  Create a priority queue pq to store the rope lengths.   */
        PriorityQueue<Integer> pq = new PriorityQueue<>();
        for (int i = 0; i < size; i++) {
            pq.add(arr[i]);
        }
        int result = 0;
        /*  Continue until only one element remains in the priority queue ie pq.size() > 1 */
        while (pq.size() > 1) {
            /*  Remove the two smallest rope lengths (ropeOne and roteTwo) from the priority queue using poll().    */
            int ropeOne = pq.poll();
            int roteTwo = pq.poll();
            /*  Calculate the combined length (combine) by adding ropeOne and roteTwo.  */
            int combine = ropeOne + roteTwo;
            /*  Update the result variable by adding the combined length (combine) to it.   */
            result = result + (combine);
            /*  Add the combined length back into the priority queue using add(combine).    */
            pq.add(combine);
        }
        return result;
    }
}

package org.wesome.dsalgo;

import org.junit.jupiter.api.Test;

import static org.junit.jupiter.api.Assertions.assertEquals;
import static org.junit.jupiter.api.Assertions.assertThrows;

public class MinCostRopeTest {

    @Test
    public void testEmptyArray() {
        // Test case: Empty array
        int[] arr = {};
        assertEquals(0, MinCostRope.minCostRope(arr));
    }

    @Test
    public void testSingleElementArray() {
        // Test case: Single-element array
        int[] arr = {5};
        assertEquals(0, MinCostRope.minCostRope(arr));
    }

    @Test
    public void testTwoElementArray() {
        // Test case: Two-element array
        int[] arr = {2, 3};
        assertEquals(5, MinCostRope.minCostRope(arr));
    }

    @Test
    public void testMultipleElementArray() {
        // Test case: Multiple-element array
        int[] arr = {2, 3, 6, 8, 10, 13};
        assertEquals(100, MinCostRope.minCostRope(arr));
    }

    @Test
    public void testDuplicateElementsArray() {
        // Test case: Array with duplicate elements
        int[] arr = {2, 2, 2, 2};
        assertEquals(16, MinCostRope.minCostRope(arr));
    }

    @Test
    public void testNegativeNumbersArray() {
        // Test case: Array with negative numbers
        int[] arr = {-2, -3, -6, -8, -10, -13};
        assertEquals(-173, MinCostRope.minCostRope(arr));
    }

    @Test
    public void testLargeNumbersArray() {
        // Test case: Array with large numbers
        int[] arr = {1000000, 2000000, 3000000, 4000000, 5000000};
        assertEquals(33000000, MinCostRope.minCostRope(arr));
    }

    @Test
    public void testNullArray() {
        // Test case: Null array
        assertThrows(NullPointerException.class, () -> MinCostRope.minCostRope(null));
    }
}

plugins {
    id("java")
    id("io.freefair.lombok") version "8.13"
}

group = "org.wesome.dsalgo"
version = "1.0-SNAPSHOT"

repositories {
    mavenCentral()
}

dependencies {
    testImplementation(platform("org.junit:junit-bom:5.10.0"))
    testImplementation("org.junit.jupiter:junit-jupiter")
}

tasks.test {
    useJUnitPlatform()
}

Complexity Analysis

Time Complexity: The time complexity of the minCostRope method is O(n log n), where n is the number of elements in the input array.
Space Complexity: The space complexity is O(n), as we need to store all elements in the priority queue.